アナログゲーム即売会「ゲームマーケット」に出展します。
- 名称:ゲームマーケット2016春
- 開催日:2016年5月5日(祝)
- 会場:東京ビッグサイト西3・4ホール
- 開催時間:10:00〜17:00
- 入場料:1000円
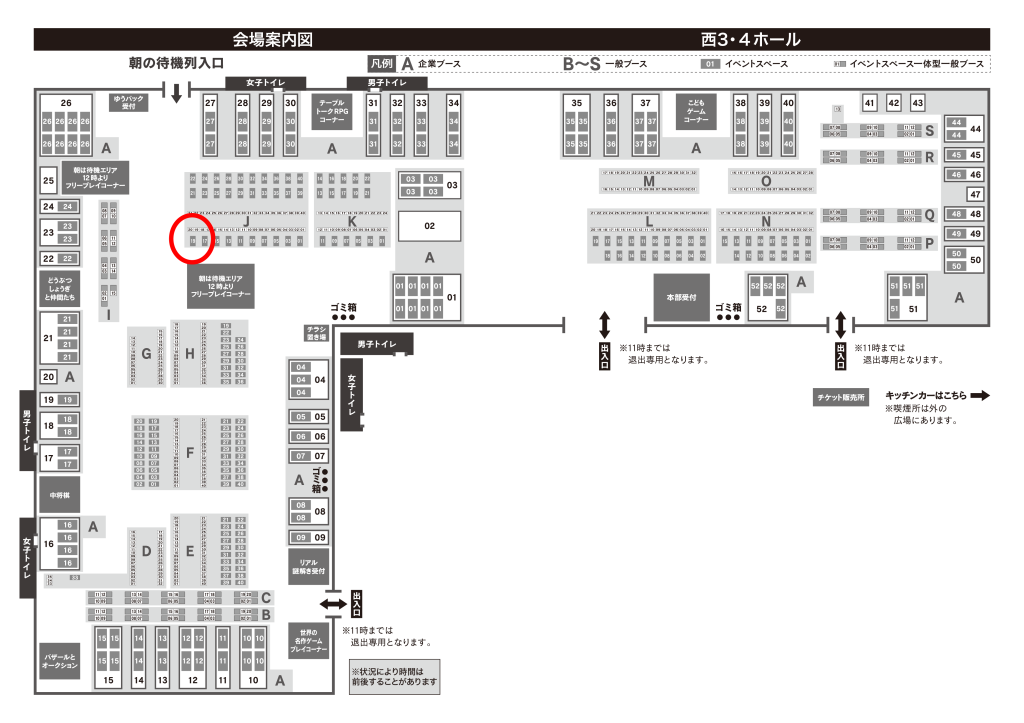
- J19-20「スパ帝国」
品薄だったナショナルエコノミーを大量に持って行きます。その他過去作も一応。今回は試遊卓もあります。

( ・3・)あたまのたいそう(・q・ )
貴重である以外に実用上の価値が無く、経済力を衒示するための商品をヴェブレン財と呼ぶ。要するに「俺はこれが買えるぐらい金持ちだぞ!」と見せびらかす貴重品である。名刺と一緒に預金通帳を持ち歩いて会う人全てに見せるより貴金属のアクセサリを身につけている方が楽に同じ目的を達成できる。
ところが金持ちの度合いがある段階に達し、全ての人が知っているほどの名士になるとそうした衒示は必要がなくなる。ヴェブレン財を持っていようがいまいが金持ちであると知れ渡っているからである。カダフィ大佐が外国滞在時にテントに泊まっていても「あの人ホテルも取れないぐらい貧乏なのかしら?」と思われたりはしない。
それどころか、むしろヴェブレン財を買わないことによって「ヴェブレン財を買って経済力を衒示する必要がないほど知れ渡った金持ちである」ということを衒示できる。つまりヴェブレン財の不在というヴェブレン財が理論上生じうる。非常に成功したビジネスパーソンなのに質素な格好をしていると精神的にも豊かに見える。
言うまでもなくこの理屈は無限に入れ子にできる。つまり金持ちである事が知れ渡った名士のクラブで1人だけ成金の様な格好をしていれば「ヴェブレン財を買わない事によってヴェブレン財を買う必要がないほど金持ちである事が知れ渡っている事を衒示する必要がないほどの名士である」という衒示ができる。という事はその中であえてヴェブレン財を買わない事によって……
事故を減らすために非常に感度の高い自動安全停止装置を導入すると、始終誤動作して業務の妨げになった挙句現場の判断で勝手にスイッチを切られるので却って安全性が低下する。同様の理屈で煩雑な確認手順が徐々に省略されたり、長いパスワードが紙に書きとめられて漏洩したり、それ自体が問題を起こすウイルス対策ソフトがアンインストールされたりする。
これらの事象は安全の為のコストが便益を上回っている場合に生ずると考えられる。ここから「コストを度外視して安全を追求する場合でもコストを度外視できない」という第二のパラドクスが導かれる。
古典的作劇手法において、破滅は破滅を防ぐ努力によって引き起こされる。巫女の予言に従って子供を殺そうとしたら逃れて暗殺者になったり、小惑星を叩き割ったら破片が地球に落ちたり、タイムマシンで過去の事故を防ぎに行ったらタイムマシン自体が事故原因だったりするのだ。
これは物語に説得力を持たせる試みの帰結であると考えられる。読者を納得させるには登場人物が危機を防ぐために最大限の努力をせねばならない(さもなくば間抜けの自滅で終わる)。ハッピーエンドであれば「破滅が防がれた」という結果を以て努力の証にできるが、破局で終わる場合は「努力が不十分だったのではないか」という疑念が生じてしまう。そこで破滅を防ぐ努力をすればするほど破滅に近づく構造を導入しておくと、破局を迎えたというまさにその結末によって充分な努力が行われたと示せる。
従って歴史が充分に皮肉に富んでいれば、AIによる人類の滅亡はAIが反乱を起こそうとしていると勘違いした人間が機械を叩き壊してしまったせいで生活が立ち行かなくなるという経緯を辿るはずである。
問1:ある人が財布を盗んだ嫌疑で逮捕された。この町の警吏は3回に2回は真犯人を捕まえる事で知られ、あとの1回は間違って無関係の人を捕まえてしまう。またこの町の泥棒は3回に1回は捕まる前に盗んだものを隠しおおせる。身辺を捜査したが盗まれた財布は出て来なかった。この人が有罪である確率はいくらか?
問2:今度は警吏が邪悪である。3回に2回は真犯人を捕まえるがあとの1回はそうと知りつつ無辜の人を捕まえて来る。しかもその場合は2回に1回の割合で証拠品を捏造し被疑者の周辺から「発見」する。それ以外は問1と同じ条件だとして、この人が有罪である確率はいくらか?
問3:警吏が輪をかけて邪悪である。無辜の人を捕まえた場合は常に証拠品を捏造する。それ以外の条件は問2と同じだとして、この人が有罪である確率はいくらか?
答1:40%
答2:約57.14% (4/7)
答3:100%有罪である!
( ・p・)<え、なんで捏造してる方が有罪の可能性高いん? (・ε・ )
冤罪云々は一旦忘れて問題を次の様に変形してみよう。
4/10 = 40%である。3つの箱に18個の玉が入っており、引く確率は全て1/18ずつで同じである。白玉10個のうち6個は箱Aに入っており、残り4個はBとCに入っている。よって箱Aからそれを引いた確率が6/10、BまたはCが4/10。
4/7 = 約57.14%である。今度は白玉が合計で7個しかない(Aに3個、Bに2個、Cに2個)。Aからそれを引いた確率が3/7、BまたはCが4/7。
4/4 = 100%である。白玉はBとCの箱にしか入っていない!
要するにこの問題は事後確率を求めるものである。箱BかCを選ぶ確率は2/3だが、「白玉を引いた」という情報を考慮に入れるとそれより下がる。箱Aの内容分布がBCに近づくに連れてこの情報は影響が薄くなり、AにもBCと同じく白玉2個と黒玉4個が入っている場合には引いた玉の色が全く確率に影響しない。この場合は最初に箱BCを選ぶ確率と同じ2/3が答えになる。箱Aの白玉の割合がBCよりも少なくなると、今度は情報の影響が反転してむしろBCの確率を高める。例えば箱Aが白玉1個黒玉5個であれば4/5が答えである。
先の問題が直感に反しているのは、真犯人が財布を隠しおおせた場合には警吏が証拠を捏造しないという非現実的な前提が含まれているせいである。証拠品が見つからない場合に常に同じ割合で捏造するのであれば有罪確率には影響しない(問3は0/0で定義不能になってしまうが)。
( ・p・)<ぱらどっくす 体操になったかな?>(・ε・ )
Tweet